別の掲示板に私が書いた内容ですが、こちらに書いておきます。
価格コムが好きだという理由もありますし、価格コムの多くの人とのやり取りの仲で考えが生まれたものでもあるからです(皆さんにお礼申し上げます)。
まあメーカーの技術者はこんなこと当然知っているのでしょうけど、ネットの世界では見ないので、それなりに有意義かと。
オーディオCD は 44.1kHz とかのサンプリング周波数がありますよね。
詳しい説明は省きますが、デジカメの世界には空間周波数という概念があります。
人間の視力の空間周波数を求め、サンプリング定理を適用することで「視力と画角の関数としての画素数」を求めることができました。
簡単に言えば
「肉眼の解像度(=視力)を十分満足する画素数を求めると、(その画素数は)視力と画角の二つだけで決まる(残りは係数)」
というものです。
例えば「斜め解像はどうする?」など、種々雑多の条件は「係数」に吸収されますので、結局のところ画素数は視力と画角の関数となります。
以下、結果だけを示します。
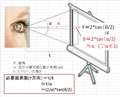
視力を n、その視力によって見える角度を α とおく。
α = (π/2)*(1/90)*(1/60)*(1/n) = π/(10800*n)
水平方向画角を θH、垂直方向画角を θV とおくと、求める画素数 N は
N = (((2*n)/α)^2) * tan(θH/2) * tan(θV/2)
= 466560000 * (n/π) * (n/π) * tan(θH/2) * tan(θV/2)
「視力の2乗に比例し、半画角の正接の2乗に比例する」という結果となります。
※この関係式はデジカメの撮像素子だけでなく、液晶などのモニターにも適用されます(画角は鑑賞画角と呼ばれる)。
わかりやすいようにフルサイズ換算何ミリの画角、というのを x とおき、各アスペクト比ごとに計算式を書いておきます。
N = ((10800*n)/π) * ((10800*n)/π) * RH * RV * (1/x) * (1/x)
4:3の場合:RH = 34.6, RV = 25.95
3:2の場合:RH = 36, RV = 24
16:9の場合:RH = 37.7, RV = 21.2
例えば視力1、アスペクト比3:2、換算35mm画角だと(x = 35 として)、
N = ((10800/3.14)^2)*36*24*((1/35)^2) = 8335380
約 833 万画素
となります。
サンプリング定理から求めたので、カラーフィルターの無い白黒撮像素子、ローパスフィルターなども排除した状態の画素数とお考えください。
以降は補足説明をしていきたいと思いますが、超ゆっくりペースになるかもしれませんので、ご了承ください。頭の中で理解の目途が立ったので書き込んだわけですが、実際に文章化するのは大変とかの理由です。
質問・突っ込みももちろん歓迎しますが、すぐには返事できないかもしれません m(_ _ )m
書込番号:8264332
![]() 1点
1点
やっぱり間違いあり。訂正します。
>N = (((2*n)/α)^2) * tan(θH/2) * tan(θV/2)
正しくは
N = ((2/α)^2) * tan(θH/2) * tan(θV/2)
です。
書込番号:8264341
![]() 0点
0点
私は難しい計算は苦手なのですが
経験上 懸垂幕などの大判印刷であっても600万画素あれば
クライアントっさんは文句を言わない
と感じています。(それなりの処理はしますが)
書込番号:8264620
![]() 0点
0点
面白い考察ありがとうございます。
ぱっと見た目ではすぐに理解できそうにないので、時間をかけて考えてみたいと思います。
式を見た感じでは、使用している式は視力の定義式において距離を画角に変換し、そこから人間が認識できる最小の空間分解能を求め、それを画素数で表している、という風に見えました。
そういう理解でよろしいでしょうか?
書込番号:8265514
![]() 0点
0点
みなさん今晩は。
私は興味を持ってくれた方全員に理解してもらいたい、「わかった」というあの感動を共有したいと思ってますが、なかなか説明って難しいんですよね。
例えば数学アレルギーの方に理解していただくには高校数学を説明せねばなりませんが、説明下手だと木を見て森を見ずに陥ってしまう。
内容そのものはわかってしまえば「な〜んだ」なんですが、こういう物理現象の考察にはきちんとした定義付け、条件設定をしないと途中で躓きます。かと言って話の全体像を把握する前だと理解されないし。
とりあえず アナスチグマートさん 宛てに簡単に説明しておきます。
焦点距離(鑑賞距離)x 先にある撮像面(モニター)において、視力 n の人は αx の幅を見分けられる。
画素ピッチを αx にするとサンプリング周波数は空間周波数の二倍になる。よって
N = (RH/(α*x)) * (RV/(α*x))
端折って説明するとこんな感じです。
あとは(好みですが)変数を減らして式を美しくする。美しくするためだけでなく、シンプルにするとそれが本質と気付きます。
「350dpi で A3 にプリントした写真を適切な鑑賞距離をおいて」ってのは本質を見失ってると考えます。
ま、これを言うにはちゃんとした前提条件を設定せねばなりませんが。
書込番号:8268969
![]() 0点
0点
自分で書いてて気になったのですが、
>簡単に言えば
>「肉眼の解像度(=視力)を十分満足する画素数を求めると、(その画素数は)視力と画角の二つだけで決まる(残りは係数)」
>というものです。
これ非常に文学的な表現で、論理の面からはいまいちですね。
「以下の式で求まる画素数 N は、その画角において視力 n の人の空間周波数を表現する十分条件」
ってのが正しいのでしょうが、ちんぷんかんぷんさは否めません。
「数式とサンプリング定理がすべてを語る」なんで、元々説明には適さないのですよね。
ということで、論理的厳密さを求めることがいいかどうかという例でした。
書込番号:8269038
![]() 0点
0点
良く言われている「キャビネサイズを約25cmの距離から鑑賞する」と言う場合だと
・180mm×130mm(キャビネサイズ)
・250mmからの対角画角が約47.9度
これを35mmフィルムサイズ換算だと48.7mmに相当しますよね。
じゃぁ、世間で言う「適当な鑑賞距離」は、今回の式においては「(35mmフィルムカメラにおける)50mmの画角」というのを対応させればよいのですね。
勘違いだったらごめんなさい。
視力1.2の人で上の条件だったら
N = ((10800*1.2/3.14)^2)*36*24*((1/50)^2) =
5887412
で、600万画素が十分な条件というのが求められる関係式ということでよろしいでしょうか。
書込番号:8269105
![]() 0点
0点
50mm 画角で視力1.2 で、計算違いが無ければその通りです。
前提条件が一杯あるのでどれから書いてよいかわからないのですが、私の求めるのはリアリズムなのです。
「肉眼で見えてるの風景は細かい部分が解像してるのに写真に撮ると解像してない」
これはリアリズムに反します。
広画角で撮影した写真を狭画角で再生。これもリアリズムに反します。
広画角で撮影した写真を同画角で再生したいが、現実問題モニタの画素数が足りないがゆえに、元の写真を切り取ってピクセル等倍で鑑賞。結果狭画角になった。これは視野が狭くなっただけでリアリズムです。眼前に広がった風景が、同じ大きさで鑑賞時にも展開されているからです(大きさの定義が必要になりますが)。
リアリズムを求めず、鑑賞行為に私の式を適用するのは「ドットの粗さを認識させない鑑賞方法」として有効です。
しかしリアリズムでない鑑賞に「画角」が果たして重要かどうか(つながりで画素数が重要かどうか)。
むしろその場合は「ドットピッチ」と「鑑賞距離」のみが重要であるはずです(もちろん視力も)。
もちろん見る写真のサイズは固定されているので結果的に画角は出ます。
しかしリアリズムでない人の場合は鑑賞時の画角を任意に変えてそうです。つまり画角は重要な要素ではないのです。
その際鑑賞距離も変わりますが、「これ以上近付いちゃ粗くなるよ」の指標としてのみ存在します。それでももっとみたいと近付く人・ルーペまで持ち出す人もいるでしょう。
つまりリアリズムでない場合には「画素数と他の変数との関係式を作る意味が無い」のです(はっきり言えば画素数はいくつでもよい。好み)。
私の式はリアリズムを求める場合に有意義、求めない場合にはあまり価値が無い、とお考えください(自分も自信ありませんがたぶんそうだと思う)。
書込番号:8269136
![]() 0点
0点
と いうか VGA(640x480)のデジカメで綺麗に(遜色なく)
写るようにするには プロジェクターには
どれほどの解像度で投影すればいいことか という問題と同じでしょう。
(大体 1024x768かな)
人間の目(網膜)は黄点というのが存在し この視点が
最大解像度を持ちます (10cm先で0.1mmの解像度)
なのでこの距離であら捜しされるとつらいので
プリント上のいかなる点でも この解像度を維持することが
グラビアプリントには求められます。
350dpiとかという数値はここから計算されていますし
もし網膜のすべてを黄点なみの解像度にしたとしても
人間の目は 600〜800万画素程度といわれています。
書込番号:8269146
![]() 0点
0点
>京都のおっさんさん
丁寧なご説明ありがとうございます。
写真に対する考え方を含め、いろいろと勉強になります。
式の内容についてはまだ理解しきれていません。
時間があるときにじっくり考えてみたいと思います。
リアリズムとは、見たものをそのまま再現する、ということですよね。
そうすると鑑賞するときも撮影時と同じパースペクティブになるよう適切な距離で鑑賞する必要があるように思います。
(そうすると広角写真の再生には巨大な用紙やスクリーンが必要になってしまいますが・・・)
それままた違う話でしょうか?
書込番号:8269347
![]() 0点
0点
すみません、自己レスです。
>そうすると鑑賞するときも撮影時と同じパースペクティブになるよう適切な距離で鑑賞する必要があるように思います。
>(そうすると広角写真の再生には巨大な用紙やスクリーンが必要になってしまいますが・・・)
これは、
「鑑賞するときも撮影時と同じパースペクティブになるよう適切な"画角"で鑑賞」
です。
再生した印刷物やモニタの大きさに合わせ、撮影時と同様の遠近感が再現できる距離で鑑賞するということです。
この場合、広角でも近くで鑑賞すれば大きなスクリーンは必要ありません。
知りたかったのは、こういう鑑賞方法を望んでいるのか、それとも単に解像度だけの問題なのか、ということです。
書込番号:8269420
![]() 0点
0点
kuma_san_A1さん の問題について。
私はリアリズムの観点からこの事象を思考してきましたので困惑しましたが、別にリアリズムかどうかは重要ではありませんでした。
客観的な事象と主観的(感応的)な事象を混ぜて論じていたためわかりにくかったと思いますので、客観的な事象で思考します。
とりあえずここだけで通用する単語の定義をしますが、ご了承ください。
α = (π/2)*(1/90)*(1/60)*(1/n) = π/(10800*n)
この式で
n:解像度係数
α:解像度
n = 1.0 の時の解像度:単位解像度
と定義します。すべて物理量としては無単位です(解像度の単位を rad としてもよい)。
単位解像度 = 0.00029 です。
半径 x の円の(距離 x における)解像度α で挟まれた部分の円弧の長さは αx である(αx の単位は「長さ」)。
距離 x での(このベクトルを法線ベクトルとした)平面の、解像度α で挟まれた部分の長さも αx である(α が小さい場合)。この αx を「解像度ピッチ」と定義する。
横方向 αx、縦方向 αx で囲まれた正方形の範囲を「画素」とします。一つの画素の面積は (αx)^2 です(単位は「長さ^2」)。
一方、距離 x での横方向 RH、縦方向 RV で囲まれた長方形の範囲を「像面」とします。像面の面積は RH * RV です(単位は「長さ^2」)。
画素を像面に「互いが重ならないように、隙間無く」敷き詰めた場合、その画素の個数を「画素数 N」とします(単位は無単位)。
容易にわかるように
「像面の面積」 = 「画素数 N」 * 「一つの画素の面積」
です。
私の初出の式と同じですね(単位は「長さ^2」)。
ここからは面倒くさいのでざっと書きますが、
tan(θH/2) = RH / (2*x), tan(θV/2) = RV / (2*x)
を用いて、x, RH, RV の三変数を消去してください。
また、いちいち定義はしませんが、kuma_san_A1さん の問題では
画素数 = 6M, 解像度係数 = 1.2, フルサイズ相当画角 50mm
となります。
この場合は三変数のうち二つが与えられて、残りの一つの変数を求めよ、という問題が作れます(そういう命題に答えられます)。
私の示した式は法則、公式として使えることがわかります。
「視力」というのは主観的(感応的)な物理事象です。人間を被験者とした実験によりその値が求められるものだからです。
客観的な公式で感応的な事象をよく説明しうるか? はこのスレッドの一つのテーマです。
簡単な計測なら行えます(それが時間がかかるかもと書きました)。個人の感応がその結果を良しとするか、それは個人しだいですね(ここは結構複雑な問題なんです。有無を言わさない画素数は無限大しかありません)。
あ、あと、「単位解像度」って定義しといて使ってませんね(笑)。
n:視力係数
α:視力
n = 1.0 の時の視力:単位視力
って(勝手に)視力を定義し直しますと、デジカメの製品を作る場合に
「単位視力における製品画角」
なんて項目を付加することができるかもしれません(笑)。
シグマ DP1 の単位視力における製品画角は
フルサイズ換算47.48mm
って簡単に求まります。
これはどういう意味かと言いますと、
「ズームレンズを操作して 換算47.78mm画角にすると、視力係数 1.0 の人の空間周波数と同じになるよ」
です(空間周波数はまだ定義していませんが)。
DP1 は単焦点なので意味無い表記ですが(笑)。
書込番号:8270370
![]() 0点
0点
印刷は 1ドットですべての諧調を表現できるわけではありませんでしたね。
では印刷に関する記述は撤回し、考えないこととします。
印刷も「解像度ピッチ」というモデルに変換する方程式があれば、私の式に代入できますが、印刷はよくわからないので。
書込番号:8270383
![]() 0点
0点
アナスチグマートさん
パースペクティブという用語を使う場合には、パースペクティブを(自己流でも何でもいいから)定義せねばなりません。
私はパースペクティブを定義できますが、その定義によると今回の事例とは関係無いですね(たぶん)。
私はここでは今回の事例とパースペクティブとを切り離します。
書込番号:8270399
![]() 0点
0点
>この場合、広角でも近くで鑑賞すれば大きなスクリーンは必要ありません。
ヘッドギア(ヘッドマウント)ディスプレイなんかそうですね。
ただし x が非常に小さい。よって解像度ピッチ(ドットピッチ・画素ピッチ) αx も非常に小さくなります。
その解像度ピッチで求めた画素数分画素を作れるかどうか、ですね。
もう一つ、x が小さくなったときに解像度ピッチは αx で良いのか?の問題があります。
あまりに至近距離では焦点が合わないなどの問題がおきるかもしれません。
解像度ピッチ αx という、x の比例関係になる範囲での考察、これも前提条件です。
書込番号:8270418
![]() 0点
0点
リアリズム…これは以前からご主張されていたと思うので「なんとなく」わかります。
撮影前に肉眼で見分けられていた部分が写真でも見分けられるには…ということでよいですか?
美しい式で表さないけど、上記の目的で考えるなら視力1.0の換算50mmで求めて置いて、「視力の二乗に比例」して「35mm換算焦点距離と50mmとの比の二乗に反比例」でいいのかな。
先の例で視力1.2だったから、換算焦点距離25mm撮影時には2400万画素あれば充分であるみたいな。
望遠側で撮影時には肉眼で見分けられなかった部分が撮影済みデータで見分けられる可能性があるのですが、それは否定しないでください。
お察しのことと思いますが、そういう意味でのリアリズムは個人的に普段から考えていません。
書込番号:8270720
![]() 0点
0点
図もあると馬鹿な私でもちょっとは理解できるかも?
と思いました。
書込番号:8271108
![]() 1点
1点
>お察しのことと思いますが、そういう意味でのリアリズムは個人的に普段から考えていません。
ぜひ考えてみてください。
非リアリズムが kuma_san_A1さん の趣向・思想なのかどうかは明記されてないので定かではありませんが、もしそのような理由で思考をシャットアウトされるのでしたら、それは科学的な態度とは言えません。
私はこのスレッドの中でも進化していますよ。kuma_san_A1さん とのやりとりで自分がリアリズムの趣向を持って思考していることに気付かされました。
そのおかげで「視力」を「解像度(角度)」と概念を入れ替えることによって、私は自分の式が公式であることを確信しました。
その他にもあります。例えば撮影時画角と鑑賞時画角を変化させることによる何らかのパラメーターを数式化する、これが新たなテーマとして生まれました。
ただ、いろいろとテーマを増やすと寄り道になりますので。
ある程度スレッドの大筋は決めてあるのです。
on the willowさん
すいませんね。私が図示すると例の下手糞な絵になるだけなので。必要に応じて図示はしようとは思いますが。
tan とか 2乗 とか使ってる部分は高校数学ですけど、画角 とか 視力(角度としての解像度)とかってみんな三角形ですよね。三角形の相似、中学の範囲ですし、わかれば「なんだそんなことか」なんですが。
書込番号:8272609
![]() 0点
0点
元々視力も良くないのですが、思考をシャットアウトしているわけではありません。
高解像度の写真は大きくプリントしてこそ活かされると考えています。
ただ、そのように大きくプリントする目的がなければ、これまでの記述的に曖昧な「鑑賞距離」…今回これがいわゆる「標準画角」であることに気づいたのは収穫です…での十分条件を満たせば良いと思っています。
ところで、(10800/π)を(3438)に置き換えた方が楽じゃないですか?
美しくないってことなのかな?
書込番号:8272713
![]() 0点
0点
とりあえず アナスチグマートさん が考えてくださってるようなので。
人間の目はある解像度(角度)で認識するってことなんですけど、ここで
「撮影時に被写体との距離を X(ラージエックス)、レンズの焦点距離を x(スモールエックス)と置いて・・・」
ってやると、パラメーターが一個増えて解答できなくなります(これ、わかったあとにもう一度ってやったときに私も陥りました)。
あくまでも人間は「像面」を見る、というモデルを作ると私の式が出来上がります(焦点距離が短くても解像度は一定で見れる前提、それがモデル)。像面は鏡で無限解像している(ドットのような段は無い)、と考えればよいでしょう。
こうして鑑賞時に同画素数、同画角鑑賞すれば、撮影時に見た解像度で鑑賞時も見ることができます(簡単!)。
kuma_san_A1さん
>美しい式で表さないけど、上記の目的で考えるなら視力1.0の換算50mmで求めて置いて、「視力の二乗に比例」して「35mm換算焦点距離と50mmとの比の二乗に反比例」でいいのかな。
>
>先の例で視力1.2だったから、換算焦点距離25mm撮影時には2400万画素あれば充分であるみたいな。
視力という感応的な評価数値でなく、解像度(角度)という単なる(任意)数値を用いたことで公式となりました(実際、ほぼ証明できてます)。
公式となったらあとは数学で考えるのが賢いやり方です。
換算画角の式なら n と x の二変数関数です(関数値は N)。
二変数関数なので三次元座標に曲面としてプロットできます(これを誰かにやってもらえたらなあ、と思うのですが)。
簡単に視力(n)一定で考えれば、y = n の平面でグラフをぶった切ればよく、結果は
N = 1/(x^2)
の形をした曲線ですよね。
kuma_san_A1さん の例に限らず、すべての解はこの三次元曲面上の点なのです。
以前からごり押しの計算はやっていたのですが、無駄な労力というばかりでなく、こういう考え方もできていませんでした(ごり押しなんで当たり前)。公式化できたのは最近のことです。
>ところで、(10800/π)を(3438)に置き換えた方が楽じゃないですか?
これも公式のうちです。覚えちゃいました。その代わり、関数電卓は常に携帯する羽目になりましたが。暗算で大体の値を知ることも計算間違いを防ぐことになるので、両方覚えれば完璧でしょうね。
皆さんが理解できたらもう少し深い話になるので、そのときに活躍します。
でもすでに示した式が現在のデジカメ会における公式であることには違いありません。深い話って言っても「へえ」程度のものです。現状では効力が無いのです。
書込番号:8272843
![]() 0点
0点
なんか難しい話になってますが、
>視力と画角の二つだけで決まる
って、
1. 視力が同じなら14インチの画面を1mの距離で見る場合と、
28インチの画面を2mの距離場合では「十分満足する画素数」は同じ。
2. (視力は角度分解能の逆数で定義されるので)視力が倍になると、
上の「十分満足する画素数」は一次元方向に2倍、画面は2次元なので
4倍になる。
ってことですよね。
「私は老眼なので、大きな画面を離れて見たい」ってのは別にして・・。
書込番号:8273160
![]() 0点
0点
これだったらわかるかな?
自分の使っているコンデジの換算画角と画素数を公式に代入。n が求まる。
壁でも何でもいいから写す。
出てきた画像の 1ピクセルは、横方向、縦方向とも必ず解像度(角度)α で写した範囲となる。
壁とデジカメの距離を X とおく。画像の 1ピクセルは、横方向、縦方向とも必ず壁紙の Xα の長さの範囲となる。壁紙の上で一辺の長さ Xα の正方形の範囲を黒く塗りつぶす落書きをすると、撮影するとぴったり 1ドットに収められるかも。
あんまり近くの壁を写すと、表記焦点距離と実焦点距離に誤差が生じるかもしれないので注意。
うさたこさん
全部正解です。
>「私は老眼なので、大きな画面を離れて見たい」
老眼はピントが近くに合わない現象ですよね。どこまで離れるかによりますが。
視力そのものは基本的に良くなるわけないでしょうから、若い時より離れて見る(= 画角を狭くする)となると画素数は少なくても画面の精細感において(若いときに比べて)不満が出ることは無いでしょう。
一方、画素数が多い分においては(どうせ離れて見て肉眼で見えなくなるのだから)問題は無いです。画素数が多いテレビはノイズが多いとか、別の事象に付いては考慮していませんが。
書込番号:8273199
![]() 0点
0点
もう一つ。思いついたのから書いて行かないと忘れちゃうので。
どんどん書いて、誰か一人でもいいから心に響けばいいかなと。
画素数といったら画角。
(独自用語ですいませんが)
解像度ピッチ(画素ピッチ・ドットピッチ)といったら距離(焦点距離・鑑賞距離)。
こっから先は私の主観。
解像度ピッチと距離だけでは画素数は求まりません。何とつまらないことか!
実際には A3 とか、サイズは既知でしょうから画素数も計算で求まりますが。でも結局それって画角ですから。
画素数はデジカメにも液晶モニタにも書いてあります。誰でもわかる。
画角は公式で計算せねばなりませんが、まあ我慢。
画素数と画角、貧乏人は低画素数狭画角で我慢ですね、画面の精細感重視なら。結局予算しだい。
あとは うさたこさん が書かれたように、その画角の三角形を書いちゃえばいいんです。
実際には計算で出すんだから同じことですが、「うちのリビングは距離 1m しかとれないな。そのかわり小さい画面で安く付く」とか、図解してわかりますね。
書込番号:8273264
![]() 0点
0点
三角形なので「画角」という言葉には抵抗があります。
「換算焦点距離」などに直してくれるといいなぁ。
書込番号:8273294
![]() 0点
0点
kuma_san_A1さん
私は「視野角」という独自用語を上で使ってますし「画角」も自分の定義で使ってます。これらは変数名であり、適当な言葉を思いつかないので使っています(センス悪いですね)。で、定義の記述は割愛させてもらってるわけですが。
画角(rad)と換算画角(mm)は物理単位こそ違えど、一対一に対応する値です。用途・目的が違うだけで同じことですね。だから好みでいいんだと思います。角度は一般単位、換算画角はカメラ界の用語という違いが大きいですかね。
考えましたが、画角(角度)でなければならない場面は今回の例では考え付きませんでした。
深い話になると角度が必須になります。
「鑑賞距離・焦点距離一定で画角が広がると、視力係数一定の元では画素数が増える」
というような定性的な例では「画角」で考えるとわかりやすいかとは思います(もちろん換算画角でもできます)。
うさたこさん
「それだけのこと」なんです。
空間周波数やら、サンプリング周波数やらを使うのは「自己の理論の正当性を証明するため」です。
何で正当性を証明したいのかといえば、結局は自己満足ですね。
モニター再生時には、ドット境界コントラストの確かなデジタルデータを入力させれば私の式は正しいです。
一方、撮影時にはアナログの「像」を標本化(サンプリング)せねばなりません。「サンプリング定理を用いれば、正当性が証明される」だけです。
「人間の目に満足できる」かどうかは思考と実験の積み重ねでしょうね。
私の主観では、事の本質をずばり言い当てたのは うさたこさん と アナスチグマートさん だけです。
書込番号:8277892
![]() 0点
0点
> 事の本質をずばり言い当てたのは うさたこさん と アナスチグマートさん だけです。
⇒ ありがとうございます。
長い文章を読むだけの読解力がないもので枝葉末節はわかりませんが。
私の発見は、・・・図を書いてて思ったのですが、・・・
Excel 2007は使い難い!!
書込番号:8278383
![]() 1点
1点
昨日の段階で、うさたこさん と アナスチグマートさん 宛てに「お見事、素晴らしい!」ってレスしようと思ったんですけど、ついでにと図を描いたのがあまりにも汚かったので止めたのです。
うさたこさん は絵も上手だし、式のまとめ方もシンプルでうまいですね。
人間の視力をイメージ化すると、片側が細ったところてんの束ですかね。
まじめに書くと細長い四角錐の束(円錐でもいいですけど)。
書込番号:8278519
![]() 0点
0点
私が共感するのはむしろon the willowさんのコメントです。
短くて的を得ている。。。
人に理解してもらおうと思ったら、簡潔な文章で。それと図解は強力な
手段。・・というのが仕事で得られた教訓です。
>人間の視力をイメージ化すると、片側が細ったところてんの束ですかね。
>まじめに書くと細長い四角錐の束(円錐でもいいですけど)。
→人間の目もレンズですから・・・。
視覚を量子化するもどうかと思いましたが、網膜細胞がCCDの素子と考えれば
いいのかもしれません。
あっ、私も理屈っぽいな。。。
書込番号:8280092
![]() 0点
0点
>人に理解してもらおうと思ったら、簡潔な文章で。それと図解は強力
それは認識していますし自分の能力不足です。
ところてんについてはどうお考えになりますか?
現実問題、モニタからはところてんの光の束が届いていますよね。それを近くで見たらドットが見えるだけですが、ある程度以上離れたらドットは見えなくなり自然に見えるのでは?という思いがあるのですが(離れるとモアレが認識できるようになったりしますが、それは別問題として)。
で、そこからは離れていっても自然さは失われないと思いますが、離れるにつれてモニタ上の認識できる情報は少なくなります。
という感じなのではないかな? というのが経験から得られた私の感覚なのですが。
そうすると、ちょうどドットが見えなくなる距離において、その人間が求める情報が認識できる。これが人間が満足する画素数の条件なのでは?と考えているのです。
書込番号:8280274
![]() 0点
0点
すみません。お手上げ気味ですが・・・。
>ある程度以上離れたらドットは見えなくなり自然に見えるのでは?
これは、その通りだと思いますが、
>ちょうどドットが見えなくなる距離において、その人間が求める情報が認識できる。
これはどうなのでしょう?たとえば高校野球のスタンドの人文字
だって情報は認識できる。
それとね、たとえば文字を読むときには画面の端の情報は頭に
入らない。逆に写真をパッと見たときには全体のイメージが認
識され、細かいドットなどは意識されてないと思います。
要は、人間の目というのは、見える見えないのほかに、一度に
取り込める情報量が制限されているのではないか。
京都のおっさんさんの意図されているところからずれてきて
いますね。ただ、上手な人の写真はリサイズされていても
心を打ちますよね。
書込番号:8281664
![]() 1点
1点
「鑑賞時画角の最大値で、撮影時の(デジカメの)画素数は決まる」
ですね。
kuma_san_A1さん の仰るとおりです。
例えば普段、換算50mm 画角で鑑賞する人がいたとする。
たまには 75mm や 100mm の狭い画角で鑑賞するかもしれない。しかし決して 35mm や 28mm の広い画角で鑑賞する事はない。
こういう人は 50mm の画角で求まった画素数のデジカメをセレクトすればよいということです。
リアリズムの押し付けはよくありません。申し訳ありませんでした。
リアリズムの定義は「撮影時と鑑賞時の画角を揃える」ですから、確かに「望遠の否定」を意味することになってしまいますね(この場合の望遠とは、写真で見た場合被写体の解像を上げることという意味)。
あとはその画素数の求め方です。
私の式はサンプリング定理から求めました(説明はしていません)。
サンプリング周波数を二倍から上げて行って人間が知覚できるか、ですが、まだ実験方法を思いつきません。
うさたこさん
すいません。私の問いかけはリアリズムに拘泥していました。
単純に「サンプリング周波数をさらに上げて知覚できるか」が重要でした。
モニタの画素数だけを上げていってどうなるか、ですね(もちろん答えは求めません)。
書込番号:8282655
![]() 0点
0点
「デジカメの画素数は鑑賞時画角で決まる」
これを法則とします(気付かなかった)。
例えば鑑賞時、画像を拡大して画面枠に入りきらない鑑賞方法をした場合は、入りきらなくなった部分も含めて(仮想画面枠を作って)画角を再計算すれば法則は成立します。
ルーペで見るなどの場合も同様、画角を再計算します(広大な画角となるでしょう)。
自分の鑑賞時画角で差異が認知不能になる画素数があるとします。それをモニタとデジカメの画素数とすればよいということです。
デジカメの画素数がモニタの画素数より少ない場合:ボケて見える。
デジカメの画素数がモニタの画素数より多い場合 :差が無い。
撮影時画角と鑑賞時画角の大小の関係に対する、人間の「現実の風景に対する解像」と「鑑賞時の写真内の風景に対する解像」の大小関係を書きます(肉眼では見えてるのに写真だと見えない、あるいはその逆の関係)。
以下、画角は狭い・広いの大小関係。
撮影画角 < 鑑賞画角 ・・・ 現実の解像 < 写真で見る解像
撮影画角 = 鑑賞画角 ・・・ 現実の解像 = 写真で見る解像
撮影画角 > 鑑賞画角 ・・・ 現実の解像 > 写真で見る解像
一番目は望遠で撮って広角で見るので、被写体が現実以上に解像して見える。
二番目の関係がリアリズム。
三番目は広角で撮って望遠で見るので、写真では現実の肉眼の解像がスポイルされる。
被写体の解像にうるさい人は、鑑賞画角の決定時に上記のことを考慮すべきでしょう。
書込番号:8283271
![]() 0点
0点
>三番目は広角で撮って望遠で見るので、写真では現実の肉眼の解像がスポイルされる。
画素数はモニタの鑑賞画角で決めているので、元々デジカメ画像には現実の肉眼の解像は記録されていません。
上の三つの関係はいずれ式化するつもりです。
よくある(?)誤り Q&A
Q:「プリンターを A4 から A3 に買い換えたので、デジカメの画素数も倍にしなきゃいけないよね?」
A:画素数はプリントサイズではなく鑑賞画角(と視力)で決まります。
もし A3 プリントを新築の大きい部屋に飾るのなら、今より画角が狭まり画素数は少なくて済む可能性もありますよ。5年前に買った低画素デジカメが再び活躍できるかもしれませんね。
画素数がサイズで決まると、デジタル一眼レフはえらい低画素数ということになっちゃいますね。パナの FX150 が 1400万画素あります。APS-C は 3倍(面積 9倍)のサイズありますから(なのに最高でも同画素数程度ですよ?)。
Q:「広角で写すんだから解像度が低くなるよね。だったらデジカメの画素数も上げないといけないね?」
A:鑑賞画角で考えてください。鑑賞画角で得られた画素数のデジカメで撮ってください。
もしそれで「なんか写っている情報が少ないな」なんて感じられたら、デジカメを望遠で撮ってください(いわゆる普通の意味での画角は狭まります)。
画角が狭くなるのはいやだ(焦点距離が長くなるのはいやだ)と言うのでしたら、鑑賞画角を広げるしかありません。もっと画面に近付くとか、大きいディスプレイに買い換えるとか(画素数は再計算してくださいね)。
こんな感じで、どなたかが HP に記載してくれると嬉しいです。自分はパソコンが苦手なのです。
今までの常識が間違っていたのですから、正しいものの見方を常識として広めたいものです。
書込番号:8284833
![]() 0点
0点
>サンプリング周波数を二倍から上げて行って人間が知覚できるか、ですが、まだ実験方法を思いつきません。
狭画角で見れば知覚評価試験できますね。
液晶モニタの画素数と視力から画角を計算。それより狭い画角で見ればいいのです。
たいていのデジカメはモニタ画素数より上。
視力 2.0 として、私のモニタだと換算画角 193mm と出ました。倍の 386mm で見れば画素数は 1/4 でよい。一旦その画素数まで縮小して、モニタ画素数まで拡大して鑑賞 ← 擬似的なサンプリング周波数二倍の例。
それとモニタの画素数まで縮小した画像 ← サンプリング周波数四倍の例。
両者の比較で差があるか? です。
簡単に言えば、モニタのドットピッチ 0.3mm の場合、視力 1.0 の人が 2m の鑑賞距離でやれば同じことができます。
書込番号:8288306
![]() 0点
0点
京都のおっさんさん
私は別アプローチで、視力測定のランドルト環で考えてみましたよ。
ランドルト環は5m用で直径7.5mm、太さ1.5mm、切り欠き幅1.5mmです。
視力1の人がこれを見たとき、視野角は1/60度とのこと。
これと、人の集中時視野を46度と合わせて考えれば、46×60=2760ピクセルが視力1の識別できる
ギリギリのピクセルサイズではないかと思うんですよ。
視力2の人はランドルト環の直径が1/2まで識別できるそうですから、2×46×60=5520ピクセルが識別限界。
一辺の識別能力ですから、画素数換算で行くと、視力1用で600万画素、視力1.5用で1300万画素、
視力2用で2400万画素くらいが限界という結果になりました。
コントラスト知覚ですから、これ以上の精度は必要ないとは思うのですが、どうでしょうか。
例えばA4の紙を全体識別できるギリギリの近距離で置き、印刷精度を240dpiと考えると、
概ね2800ピクセルと一致するんですね。240dpiは商業カラー印刷の最低ラインですから、
なんとなく納得も行きます。
書込番号:8311133
![]() 0点
0点
Satosidheさん
仰るとおりで、個人的には「十分以上の画素数」なんです(視野角についての認識は私と違うのですが)。
世の中にはいろいろな人がいます。大して考えずに「300万画素」とか「何億も必要」とか。
それらを全部論破するには順番に、だったんですけど・・・。
正直言って画素数については大体わかっちゃったんで、書くのが面倒くさくなっちゃったなと(すいません)。わかってしまったことには興味を失う、みたいな。
そのうちパワー出して残りを書き上げちゃおうと思ってはいるのですが。
とりあえず私の関係式は「画素数」と「解像限界角度」と「画角」の関係ですので普遍的に成り立つ「当たり前」のことです。
あとは「解像限界角度をどうすんの?」ってだけの話ですよね。
「高精細な画像鑑賞のための画素数の条件は?」の答えは
縦横の必要条件:私の初出の式の N 以上。
斜めの必要条件:私の初出の式の二倍の 2N 以上。
十分条件 :画像ごとに認知限界評価試験をしましょう。
です。
で Satosidheさん は「N も必要無いんじゃない?」だと思うのですが。
で、私も実際やってみて同じ意見です。
でも、見れちゃう以上「論理としては N 以上必要」って書かなきゃな、ってとこです。
この辺の話を「ピクセル等倍鑑賞」の話題を絡めながらやっていこうとは思ってたんですけどね。
まあ「まだ見ぬ未知の画素数は、画角を狭めることで知覚評価試験ができる」ので、興味のある方はやってみてください。
当然、N 以下の低画素数についても知覚評価試験できます。
書込番号:8311434
![]() 1点
1点
人間の視野角の話題が出たので、簡単に書いておきます。
視力は一般に「平面角(rad)」のこととされていますが、写真においては「立体角(str)」であらわすべきです。
「視力 1.0 の画素ピッチはいくつで、じゃあ画素面積はいくつ」と、「面積」が出てきた時点で既に「視力は立体角」なんです。
立体角で面積を出す。その領域内を一本の「視力線」が通ると考える。
面積の逆数は「面積密度」。視力線は空間のどこも均等(ぐるっと見回すので、4π ステラジアン全部均等)。つまり「面積密度一定」です。
っていう物理モデルを前提としているわけです。
ここまで書くと「私の式の間違い」に気付く人もいるかと思いますが、それは「深い話」ってことで(繰り返しますが、私の式に間違いはありません)。
書込番号:8311517
![]() 0点
0点
>私の関係式は「画素数」と「解像限界角度」と「画角」の関係ですので普遍的に成り立つ「当たり前」のことです
論理的思考が後から着いてくるタイプなんで。自分はあまり頭が良くないのです。
デジタル映像機器の解像限界角度を 360度法で n (度)とおく。
縦横を解像する画素数と画角と n との関係式は
画素数 = (tan(θH/2)) * (tan(θV/2)) * ((tan((n*π)/360))^(-2))
これなら教科書に載せられますね。
n が非常に小さいとき
tan((n*π)/360) ≒ (n*π)/360
となり「解像限界角度の2乗に反比例し、半画角の正接の2乗に比例する」という結果となります。
「じゃあ人間には何画素必要なの?」の場合には、客観的な評価数値である「視力」を用いて私の初出の式となります。
書込番号:8311810
![]() 0点
0点
>視力は一般に「平面角(rad)」のこととされていますが、写真においては「立体角(str)」であらわすべきです。
視野中心部の黄点での解像力で周辺まで考えている時点でも大きな誤差を含んでいるし
視力2.0 から 校正視力0.7(免許等の条件)までの誤差から考えたら
そんな議論になんの価値があるの?
書込番号:8312647
![]() 1点
1点
>視野中心部の黄点での解像力で周辺まで考えている時点でも大きな誤差を含んでいるし
視野中心のみで考えていますので。人間の知覚の最大部分に合わせるのです。当然の話。
>視力2.0 から 校正視力0.7(免許等の条件)までの誤差から考えたら
これは何を言っているのかわかりませんが、「視力に応じた画素数の条件」ということで独りよがりでない理論を求めます。
>そんな議論になんの価値があるの?
[8311810] で示したハードウェアの限界解像角度の式はよいですよね?
これがデジカメの教科書に載っていればよいのですけど。
視力との関係に付いては二つの面があります。
一つは何度も書いた「認知限界」です。オーディオでも 44.1KHz で飽き足らず、100KHz とかあったそうですが、それと同じことです。認知限界に達していない限り高性能を求める。それ自体は否定すべきことではないですよね? これも当たり前の話。それを考察しているのです。
もう一つは「どこまで写るか」。これを「事前に知る」です。
これは「ハードウェアの限界解像角度」の話で済んでいますね。それと視力とを絡めるのは私の趣味です。「論理的思考が後から着いてくるタイプなんで」と書きましたね。実践から思考していってこの結論にたどり着いたので、多少の話の前後はご理解ください。
「事前に知る」にはさまざまな効用がありますよ。
個人的には
「写真を撮ってみてがっかりした。原因を探ったら画素数の少なさにあった」
これが出発点でした。
画素数に限らず、私が写真に付いて思考するすべてのモチベーションは「がっかりした経験から」であり、「がっかりしたくないから」思考を続けます。
あとわりとありがちと思われる
「画素数アップで画質向上があった。果たしてどこまで画素数を上げればよいの?」
という質問に対する解答となります。
350dpi については ひろ君ひろ君さん が説明してくださったのでわかりました。「至近距離での粗探しに耐える条件」も重要だと思います。しかしそれも私の式に還元できますね(解像限界角度は変わるかもしれませんが)。
逆に画角の概念を入れないと、駅貼りポスターなどはとんでもない画素数が必要になりますよね。「プリントサイズが大きいなら離れてみる」これって結局画角なんです。
書込番号:8313012
![]() 0点
0点
おおざっぱにやりすぎてましたね。
もっときちんと出すのであれば、5m先の平面上にある1.5mm幅のコントラスト差を検出できるのが視力1の
人の視覚ですから、46度で5m先の三角形の底面を取り、だいたい水平/垂直2830ピクセルが
限界点ではないかと思います。
手前30cmに印刷物を置いて長辺25.5cm、280dpiでした。
それで計算して、おおよそ600万画素、視力1.5で1350万画素、視力2で2403万画素になりますね。
書込番号:8313649
![]() 0点
0点
Satosidheさん
すいません、あまりよく読んでいませんでした。で読んで理解しました。
考えていること、やっていることは私と全く同じです。
私の式は「人間の視野角」に限定せず、とりうる全ての画角に適用しただけです。
ところでやってみればわかりますが、視力検査ってかなり厳しい検査です。「そこまで必要なの?」って私も思います。
でも見える以上はそれを「解像限界角度」の基準に取らざるを得ない。
「ランドルト環撮影なんて写真じゃない。ランドルト環を撮るなんて狂気の沙汰だ」なんていうふうに写真を限定する権利なんて誰にもありませんよね。
書込番号:8316713
![]() 0点
0点
経験則によるインクジェット出力時の目安dpi値です。
主に駅貼りのポスターやパチンコ店など・・・
A0〜B0サイズ →100〜120dpi
A1サイズ →130〜150dpi
A2延び〜全紙 →150〜175dpi
A3延び →200dpi
A4以下 →175〜250dpi
画像にもよりますが、デジカメやスキャン4x5やブローニー版のデータをフォトショップ
上で画素数補完して、出力していました。上記サイズを超えると特に大きいサイズは、
RIPソフトでラスタライズした後、2GBの壁を越えてしまうため出力できない事もあります。
なお解像力不足でも、IJ出力の場合は誤差拡散のため、解像度不足が分かることはありません。
エッジが眠くなるため、メリハリを付けるためにコントラスト・輪郭強調を強めにかける
事で回避する場合が多いです。
書込番号:8316734
![]() 1点
1点
京都のおっさんさんの理論は、実はNHKが大昔からやっていることと同じです。
この理論上、従来テレビは画面高さの6倍が最適視聴距離、ハイビジョンの最適視聴距離は画面高さの3倍としています。
しかし実際には6倍も離れてテレビ観ている家庭がどこにあった?という問題、デジタルカメラのベイヤー配列の問題。
単純モデルとしては正しい理論でも、その先が難しくなってきますね。
書込番号:8437878
![]() 0点
0点
ソニータムロンコニカミノルタさん レスありがとうございます。
誰もこの当たり前のことを教えてくれなくて。NHK がやっていると知ってほっとしました。
最適視聴距離には当然「視力1.0 の人をモデルとする」などの前提条件が入っているわけですよね。
この先やるネタはあったのですが、気力が無くて。
とりあえず、上の式より(画素数固定で)画角を極端に広げた鑑賞法を「ピクセル等倍鑑賞」とします。
実際に上の式で求めたとおりで液晶モニターを鑑賞すると、白黒のランドルト環はその通り。なんですが、実際の風景ではコントラスト不足で肉眼で解像できないことが多々あります。
ということで、液晶のコントラスト不足という(将来は改善されるかわからないが)現実の問題が眼前にあるので、ピクセル等倍鑑賞は有効な鑑賞法です。
そして、ピクセル等倍鑑賞を前提とすると、必要な画素数は実はもっともっと少なくて済みます。
って感じで展開したかったのですけれどね。
書込番号:8438244
![]() 0点
0点
NHKは高さの7倍で計算していたはず。
昔、高柳先生のお弟子さんにそう教わりました。
書込番号:8445809
![]() 1点
1点
私の [8311810] の式を見易く書き直します。360度法の角度を「d」とします。degree の d です。
視力は「n」のままとします。視力 n の人の解像する角度は
d = 1 / (60*n)
です(単位は「度」)。
すると [8311810] の式は(換算焦点距離を「f」として)、
d = (180*(((RH*RV)/N)^(1/2))) / (f*π)
これの方が見易ければ、
d = (180/(f*π)) * √((RH*RV)/N)
従来テレビとのことなので、
N = 640 * 480
当然アスペクト比は 4:3 なので、
RH = 34.6, RV = 25.95
6倍の鑑賞距離の場合は
f = 6 * RV
7倍の鑑賞距離の場合は
f = 7 * RV
を代入してそれぞれ d を求め、
n = 1 / (60*d)
で視力を求めると、
鑑賞距離6倍:0.838
鑑賞距離7倍:0.977
と求まりました。
言うまでも無く、
「鑑賞距離6倍は、視力 0.8 の人を対象にした最適鑑賞距離」
「鑑賞距離7倍は、視力 1.0 の人を対象にした最適鑑賞距離」
です。
6倍も 7倍もそれぞれ対象としている人が違うので、どちらが正しくどちらが間違っているという類のものではありません。
視力1.0 の人の「最適鑑賞距離」で鑑賞すると、換算画角は 182mm となります(とても狭画角!)。
書込番号:8446736
![]() 0点
0点
このスレッドに書き込まれているキーワード
「デジタルカメラ」の新着クチコミ
| 内容・タイトル | 返信数 | 最終投稿日時 |
|---|---|---|
| 3 | 2025/11/11 21:17:17 | |
| 4 | 2025/11/12 1:17:20 | |
| 9 | 2025/11/11 9:29:59 | |
| 7 | 2025/11/11 20:02:55 | |
| 0 | 2025/11/08 20:24:09 | |
| 3 | 2025/11/09 13:49:44 | |
| 2 | 2025/11/08 1:38:14 | |
| 15 | 2025/11/07 3:31:06 | |
| 0 | 2025/11/05 14:51:25 | |
| 0 | 2025/11/05 14:03:52 |
クチコミ掲示板検索
最適な製品選びをサポート!
[デジタルカメラ]
新着ピックアップリスト
-
【欲しいものリスト】O11D mini v2 White SL no LCD build
-
【欲しいものリスト】やっさんのぱそこん
-
【欲しいものリスト】PC構成20251031
-
【欲しいものリスト】メインPC再構成
価格.comマガジン
注目トピックス
(カメラ)
デジタルカメラ
(最近3年以内の発売・登録)